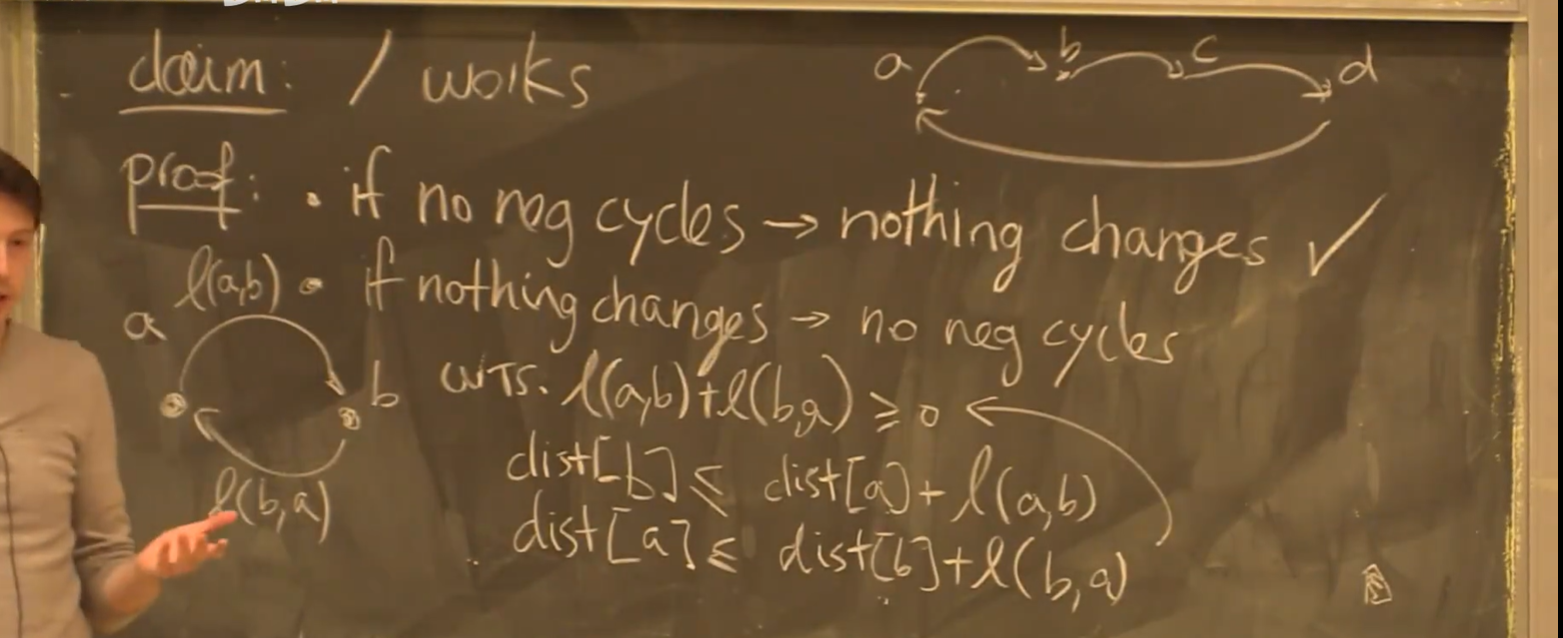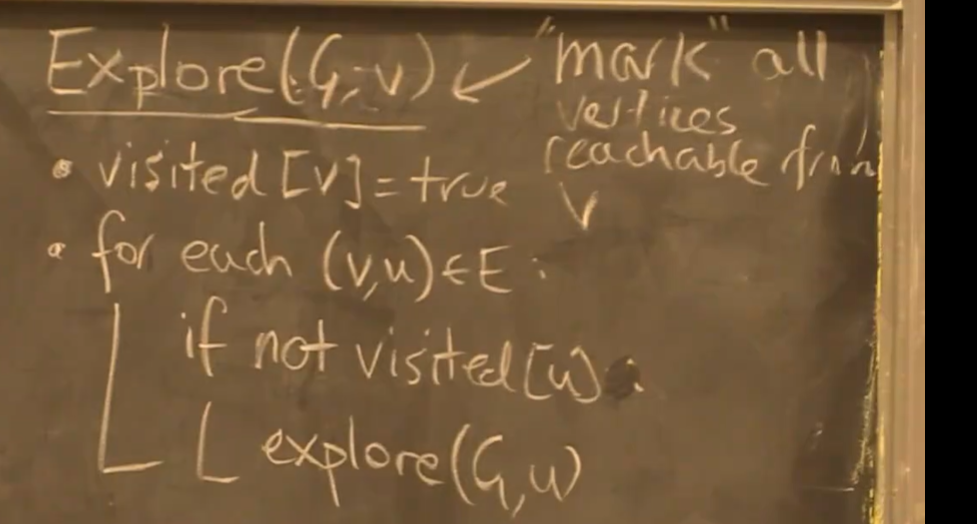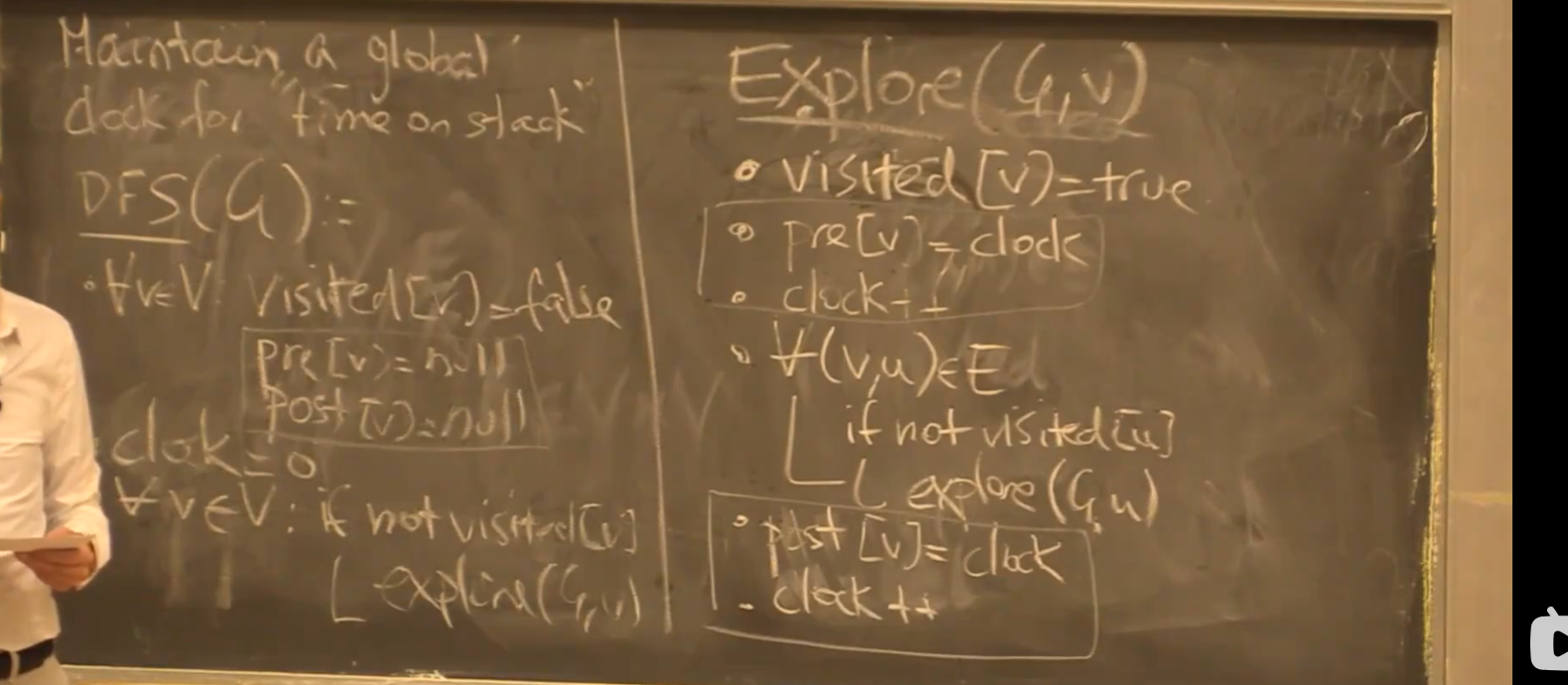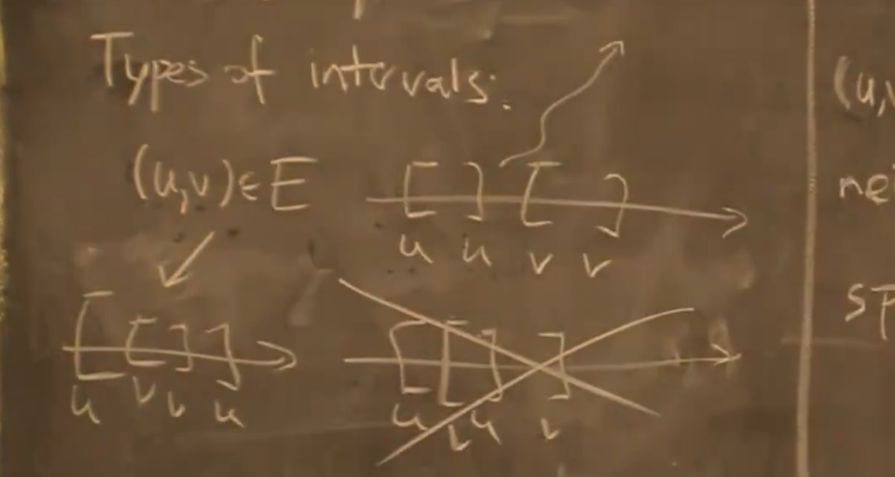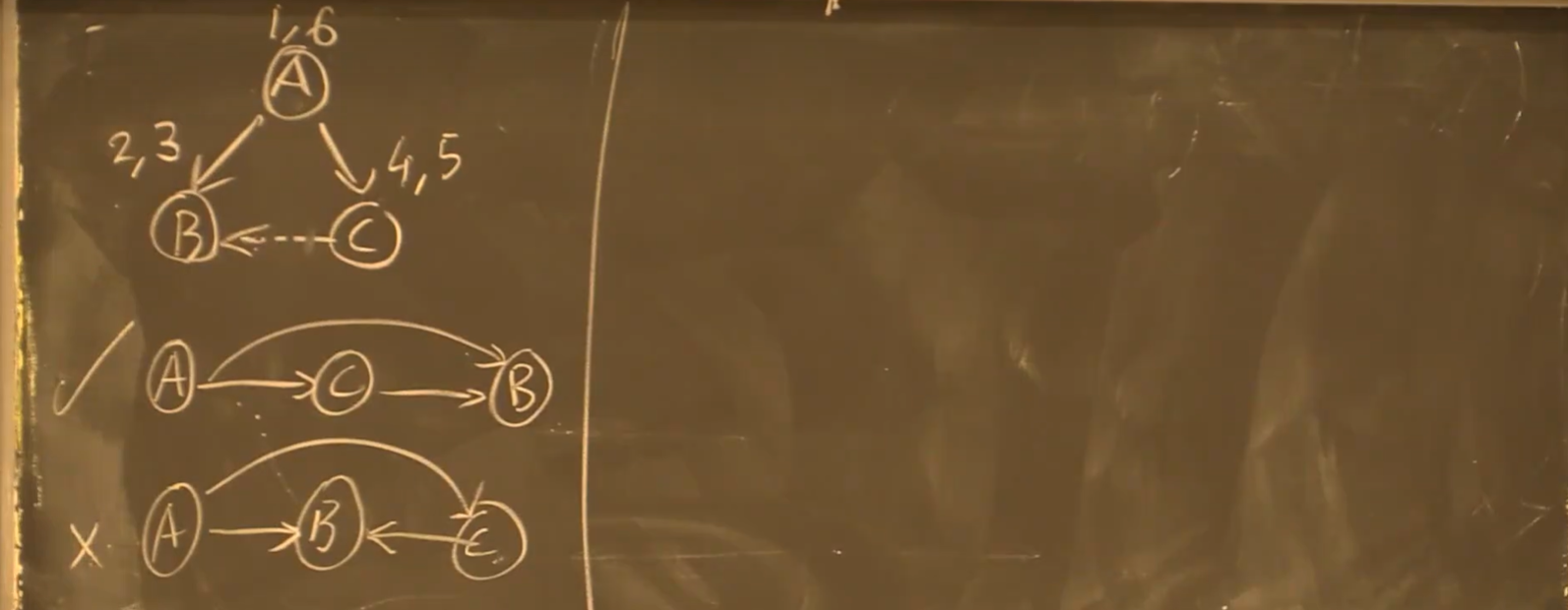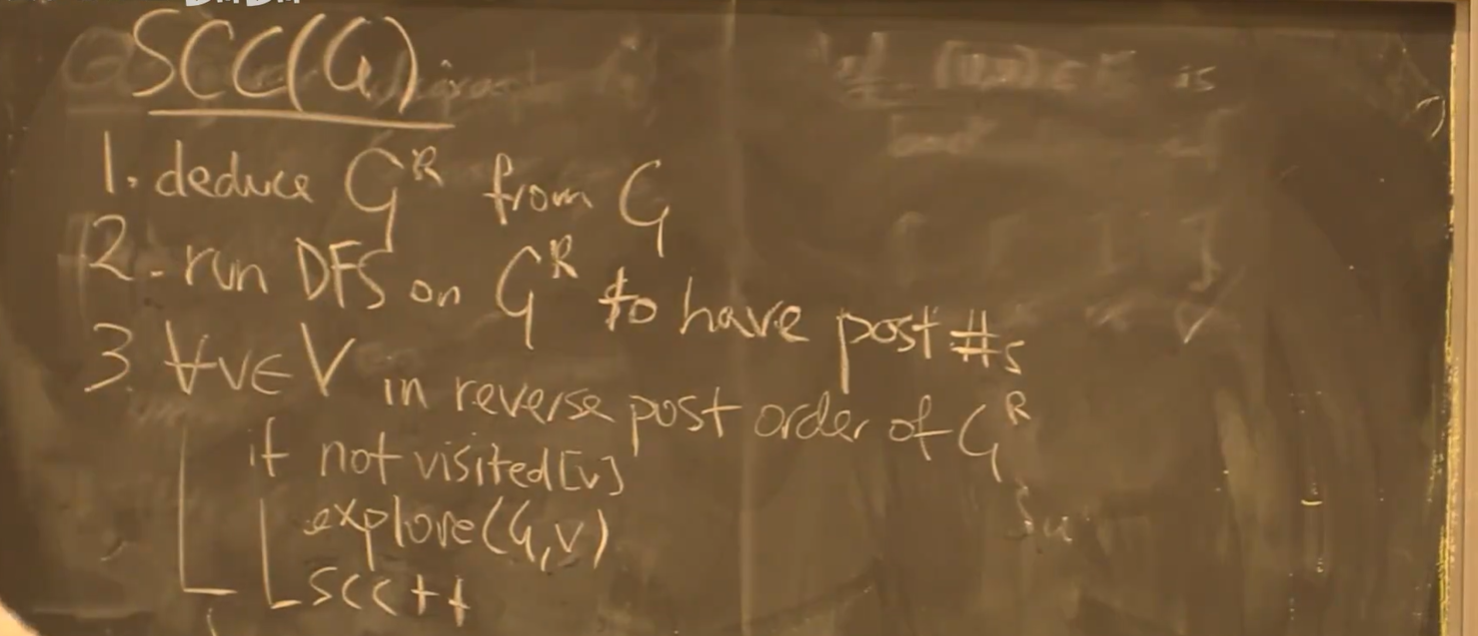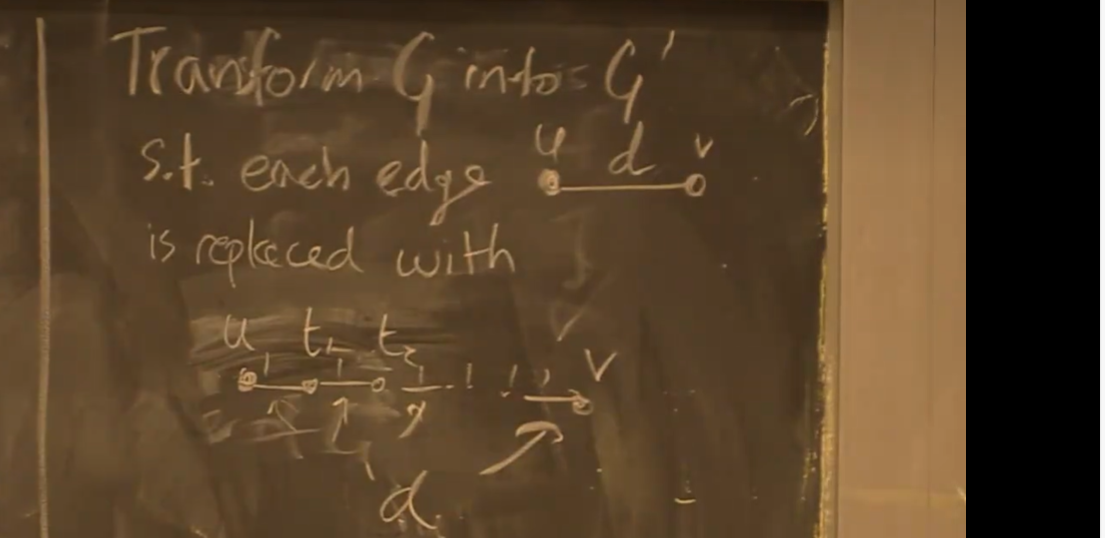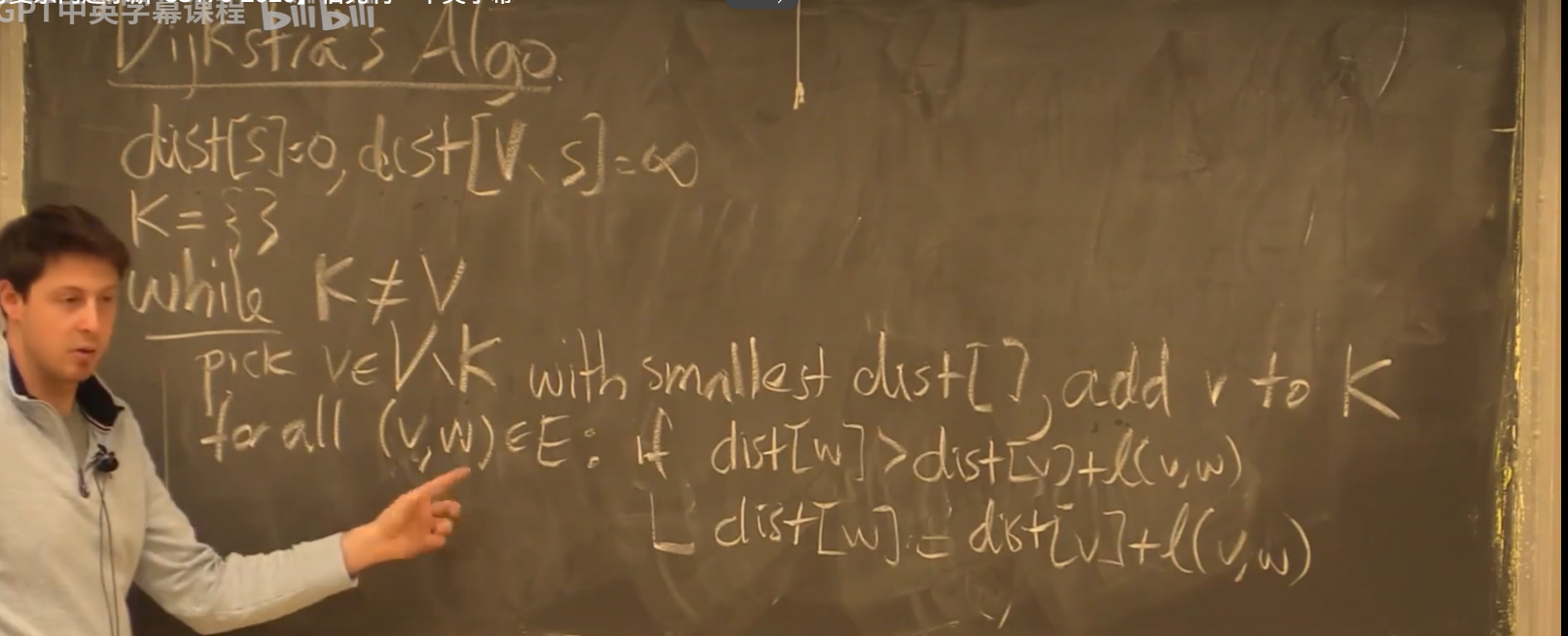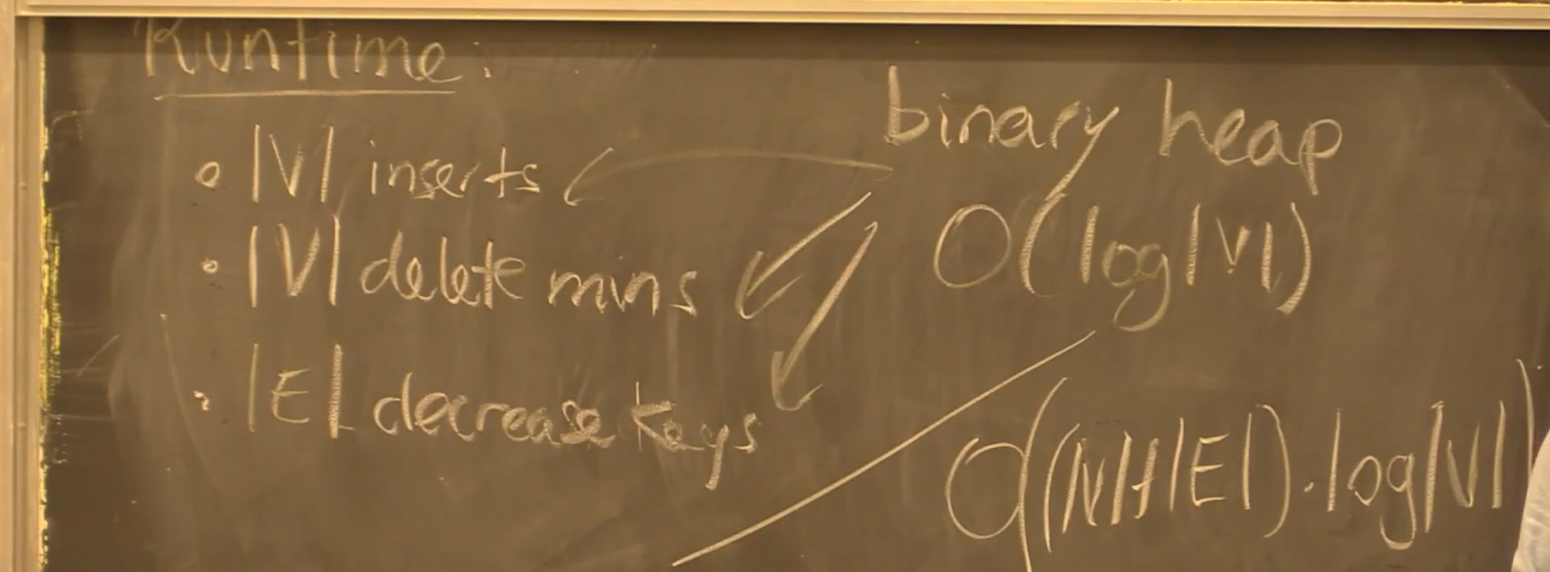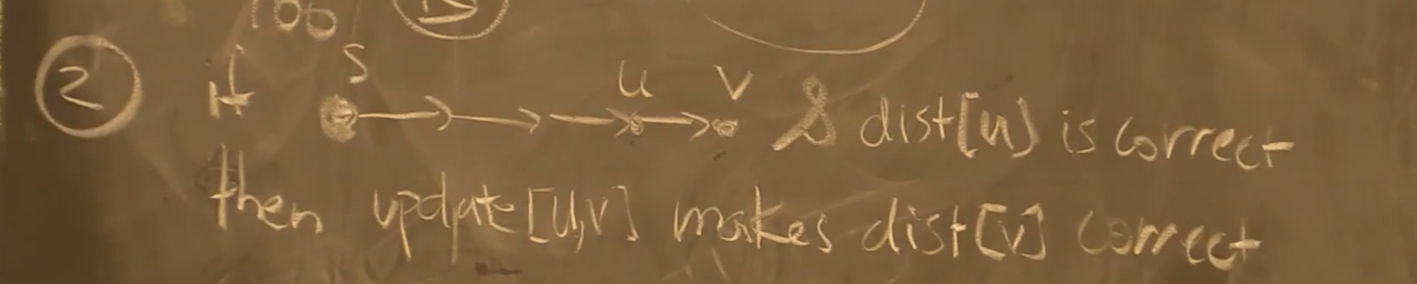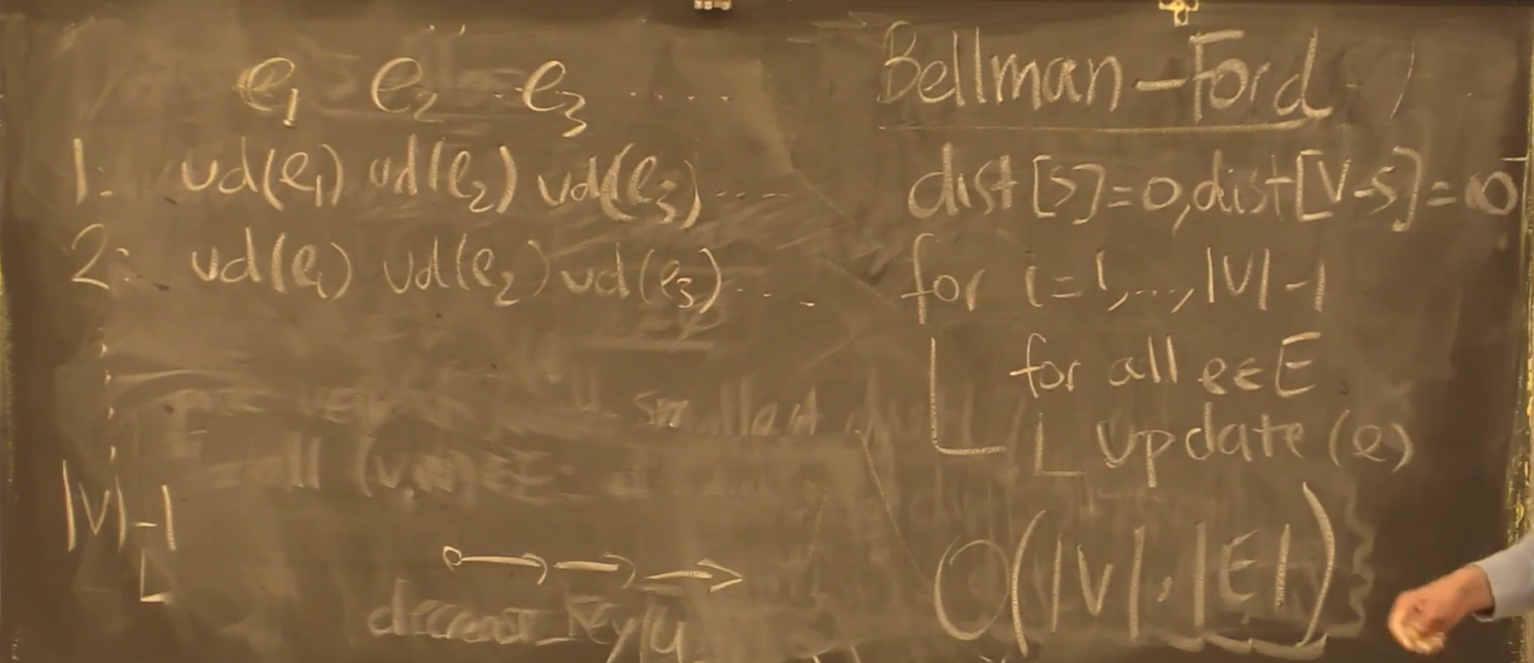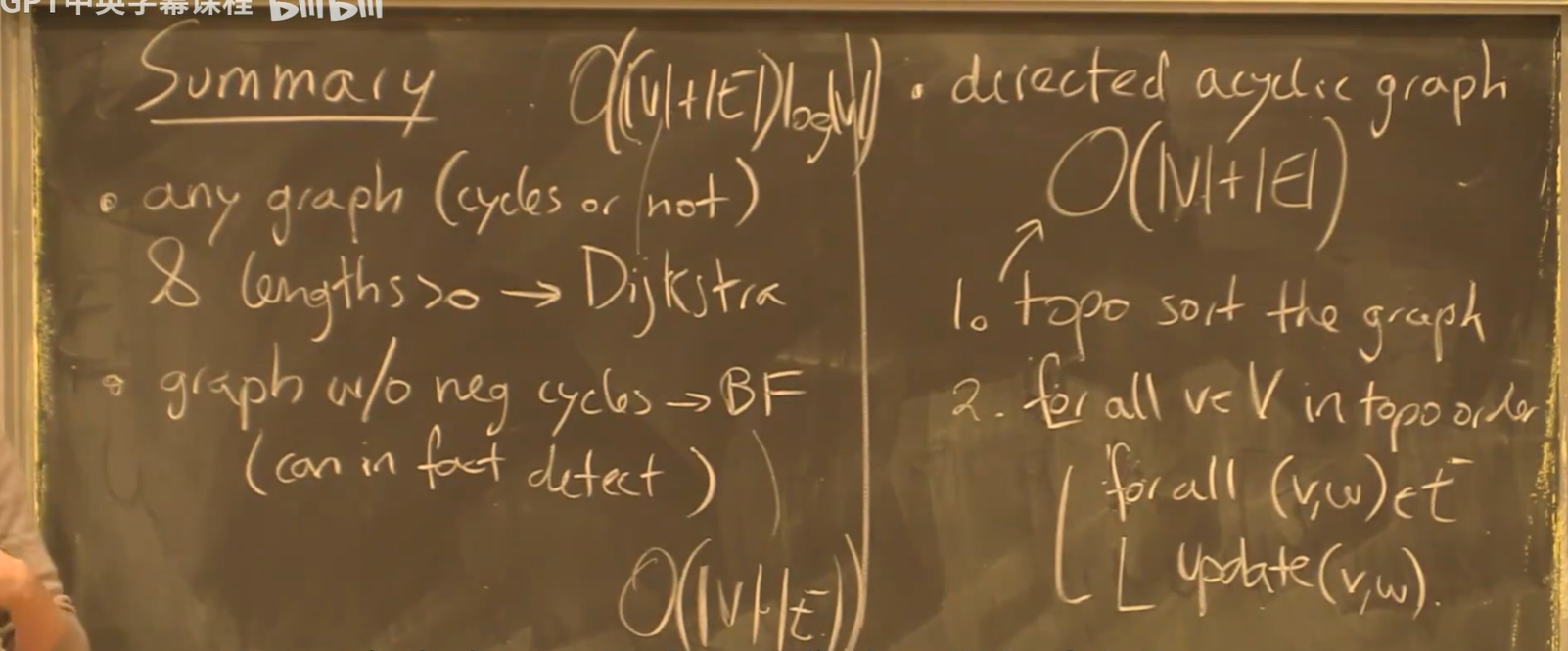图论

表示

两种表示方法：邻接矩阵、邻接表

• 一般后者用于稀疏图，前者用于稠密图
• 如何表示输入直接影响了算法的效率，需要权衡取舍

连通性

DFS

• 标记所有可达顶点，使用DFS
• 状态由栈表示

证明：DFS 已遍历了所有可遍历顶点

• 一般使用反证和路径考虑

1. 假设有一个可达、且未被访问的点a
2. 必然存在一个已经访问的点v，且有一条到达a的路径
3. 假设 b 为路径上第一个未被访问的顶点，w为b的邻接点
4. w 上运行过算法，矛盾，b是邻接点但未被访问

运行时间：$O(n+m)$

• 每个点被访问一次
• 每条边被考虑一次，无向图一条边会从两边都分别考虑一次

无向图连通分量

• 必定为强连通分量

求个数：

dfs 中标记每个顶点所属的连通分量：

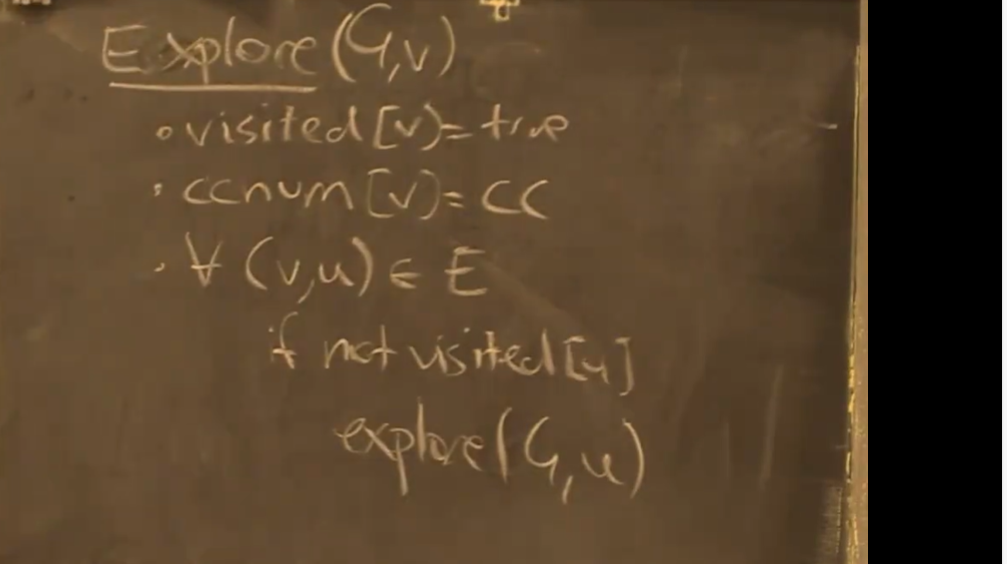
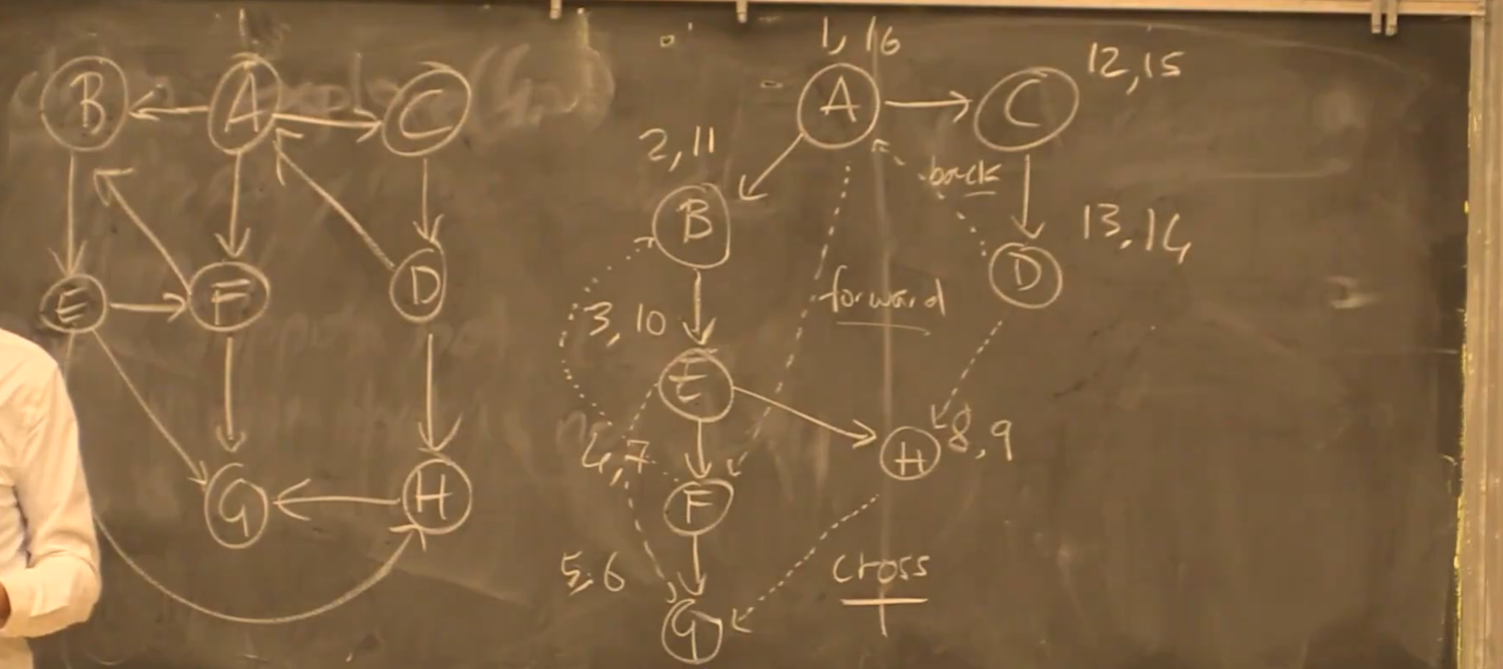
前序数、后序数

DFS中，进一步标记访问开始与结束时间：

• 全局时钟，每次进行完操作++
• pre、post 数组分别表示节点的访问开始、结束时间
  • 开始访问时赋值 pre，结束访问时赋值 post

若存在边 $(u,v)$ ，横轴表示时间，则它们看起来应该像左下角：

• 右上角表示要么不可达，要么路径上的点先前被访问过了
• 实际访问的路径边

那么对于如下的无向图，有3个连通分量：

定义：边的类型

在有向图上运行我们的算法：

• 分为虚边（不属于实际访问路径）、实边
• 虚边可以被分为：forward（指向后继）、back（指向祖先）、cross（两者有共同祖先）

在时间上表现为：

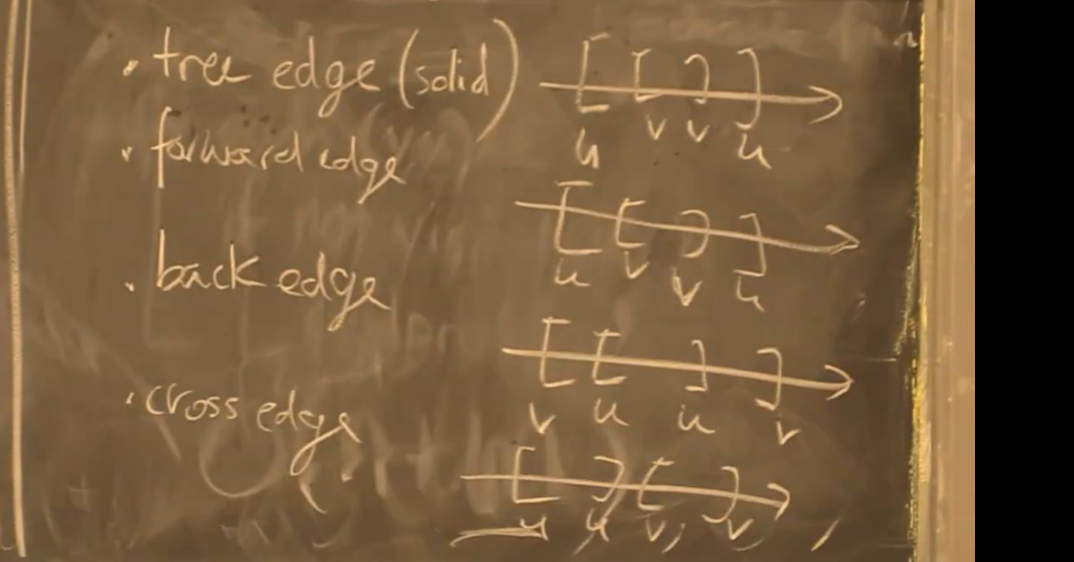
判定 DAG

一个有向图是否无环？

• 基本思路：没有反向边即无环
• 判定反向边：开始访问一个节点时入栈，结束访问一个节点时出栈，若节点在栈中且有边指向则为反向边
• 证明：

拓扑排序

• 给定DAG，使得路径上的每条边都指向前方，即不出现交叉边（DAG无后向边）

算法：DFS，按 post# 降序输出节点，即为我们的路径

• 因为先访问的顶点后弹出访问栈，那我们只需要按照弹出顺序降序访问即可

有向图分解：SCC

• 有向图可被强连通分量划分，强连通分量间组成一个DAG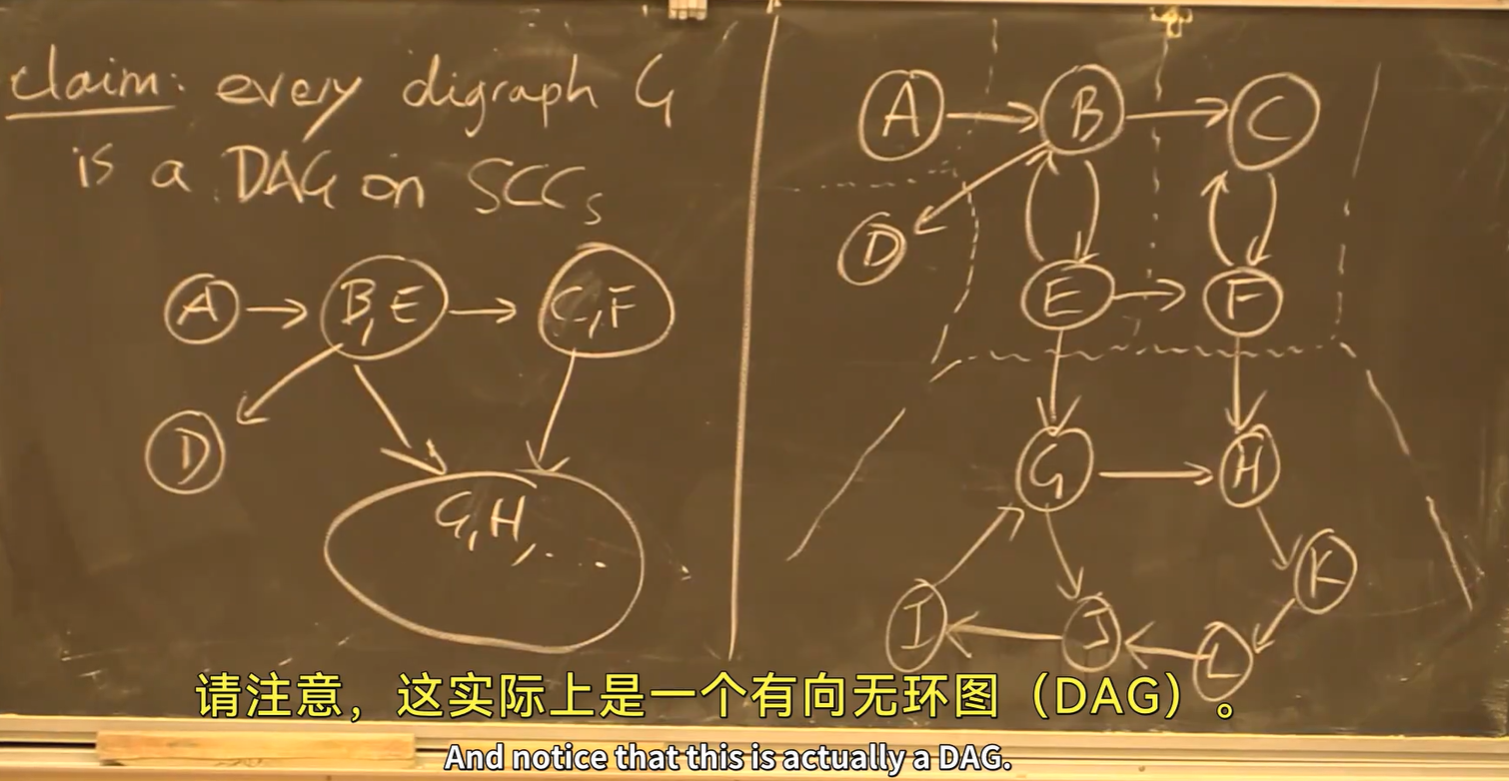： 如何寻找有向图的SCC？
• 基本思路：寻找强连通分量然后从图中移除（即mark）
• 避免溢出：强连通分量可能会溢出到其他强连通分量
  • 逆向拓扑排序顺序访问：如果按照逆向 DAG 拓扑排序的顺序访问，则必定不会溢出
  • 逆向拓扑排序顺序中，post# 最大的节点一定处在一个SCC中，且按原图访问不会溢出
• 反转图：反转图的拓扑排序顺序，即是原图的逆序拓扑排序顺序

则算法：（Kosaraju 算法）

• 反转图，DFS，得到 post#
• 按照 post# 降序访问图即可

单源最短路径

BFS

• 不断扩大源点的邻域，寻找邻居
  • 即距离为0、1、2….
• 状态由队列表示 算法：
• 距离根据上一个节点

正权重：Dijkstra 算法

一种简单算法：权重为n的边分解为n条权重为1的边，引入大量中间节点，BFS

• 速度太慢，边的权重对速度有较大影响

基于以上思想，我们可以加速边的访问，即 Dijkstra 算法

• 其基本思想是找出局部源点最短路径，并不断扩展，与BFS如出一辙
• 使用归纳法
• 注意到：K的邻点中，必定有一个节点与抵达它的边，在最终的最短路径中 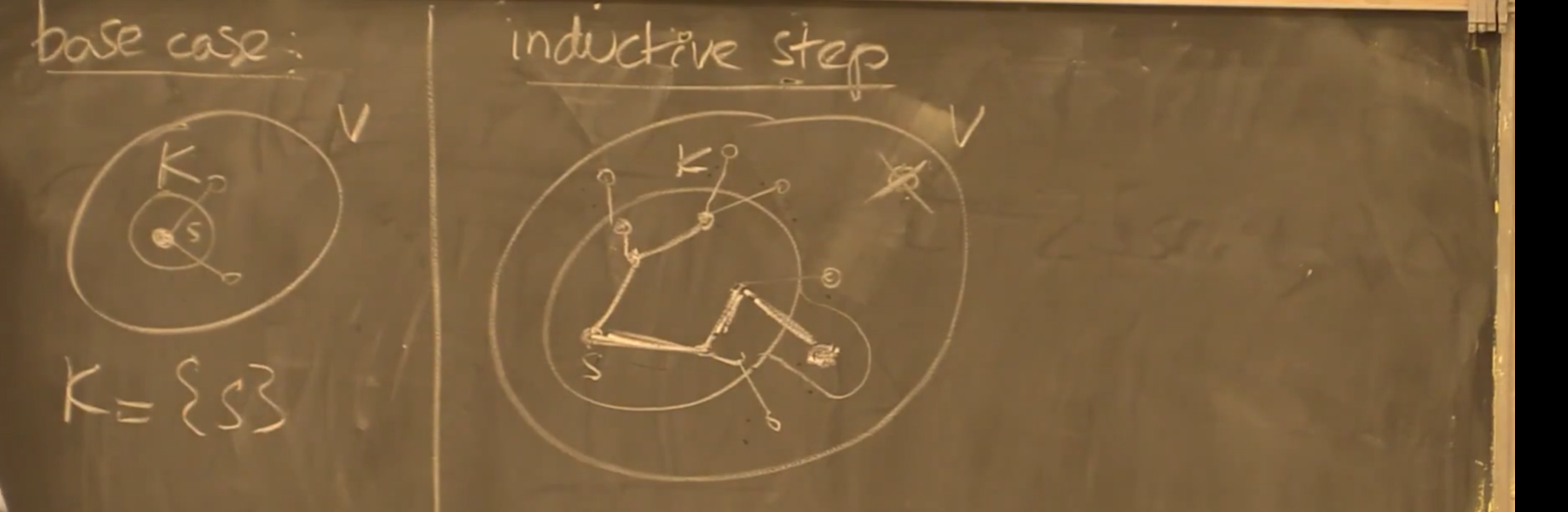维护状态：
• **dist[i]**：节点i距离源点的当前距离，会逐步收敛到最短距离
  • 初始为无穷
• subset K：包含局部最短路径中的所有节点
  • 初始为源点

算法：扩展路径+更新 dist

高效的实现：

• 从全集 U 中一步一步剔除节点，而非向空集中加入节点
• U 使用优先级队列表示，key 为 dist，value 为 node name

运行时间：

负权重：Bellman-Ford 算法

• 一种方法：转换为正权重的情形。此节中我们暂不讨论。

• 另外，存在负环的图无单源最短路径，例如：

  

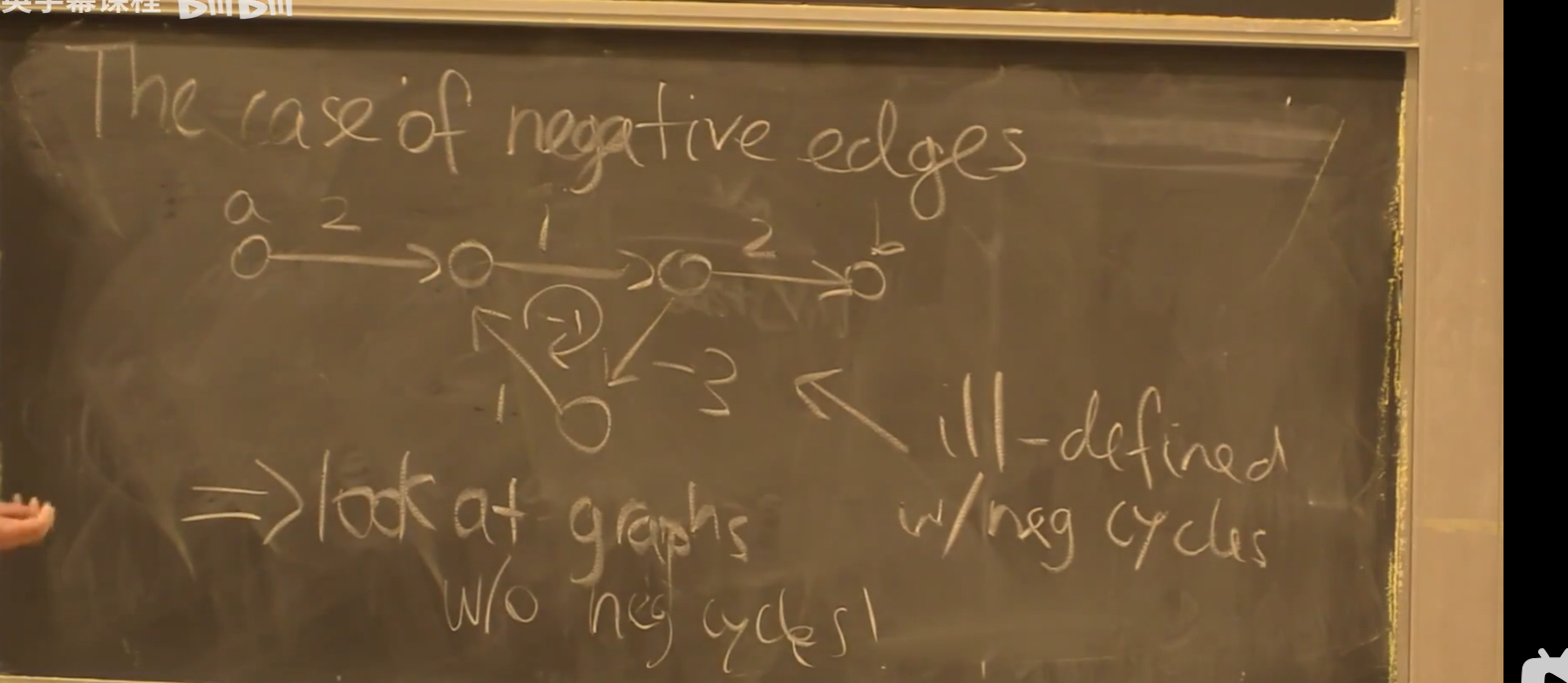
  我们关注没有负环的图；有负边不等于有负环。

• 负权重图不能仿照正权重的思路，单边扩展不再有效，例如：

  

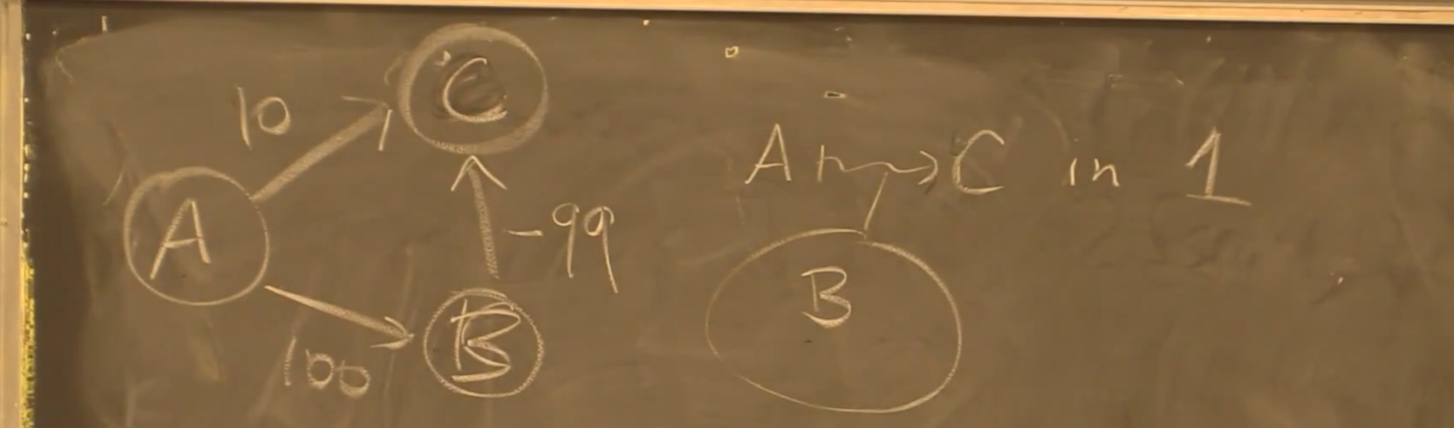
• 引理：仅当已知这条路径为最短路径时，可以进行单边扩展

  • 注：update 即 $dist[v] = min(dist[v], dist[u] + weight(u, v))$

• 注意到，执行某个算法不断进行 update，对于一个节点来说，在某个时刻一定会其得到最短路径的 update 子序列，于是我们可以得到该节点的最短路径

  • 但对于路径上的其他节点来说，该路径不一定为其最短路径

• 根据我们的引理，正确的节点从源点开始，我们查看所有的边 $V-1$ 次，便必定可以得到除源点外所有节点的最短路径距离——Bellman Ford 算法

  • 复杂度 $O(|V|\times |E|)$

负环检测：基于 Bellman-Ford 算法

• 我们已经证明了，对于没有负环的图，Bellman-Ford 算法在运行 V-1 次后，必定得到最短距离
• 若我们的算法循环第 V 次时，仍有对 dist 的更新，则存在负环
• 复杂度：$O(|V|\times |E|)$

证明：将不等式相加即可得到结果，多个节点的证明类似两个节点的证明

针对DAG的优化与总结

• 对于DAG，其单源最短路径一定按照拓扑排序的顺序访问，这就是我们的算法
  • 我们已经锚定了访问顺序，所以无需考虑单边扩展之类的问题
• 复杂度：$O(|V|+|E|)$