Hash Table
- 在我们所使⽤的hash函数中，在它的速度和碰撞率之间存在了巨⼤的取舍
- 当我们遇上碰撞问题时，我们需要通过⼀些额外的指令来解决它们
hash函数有时依然会超级快，但某些hash函数要⽐其他hash函数快2到3倍
STATIC HASHING SCHEMES
这意味着，我们需要提前知道我想要保存的key的⼤概数量。这样我就知道该如何进⾏分配，我所分配的hash table⾜够⼤能够容纳下这些key，并且最⼩化 hash碰撞，这样我也不会遇上⽆限循环或者是hash table被完全填满的情况了
（不切实际的）假设
- key 取值数已知
- 每个 key 唯一
- 无碰撞
Linear Probe hashing
- 一个大循环 slot 表，通过在表中线性寻找下一个可用的 slot 解决碰撞问题
- 需要大量的 slot
- 必须在表中存储 key，遇到下一个空位还没找到匹配的key就停
也被称为 open addressing 开地址法
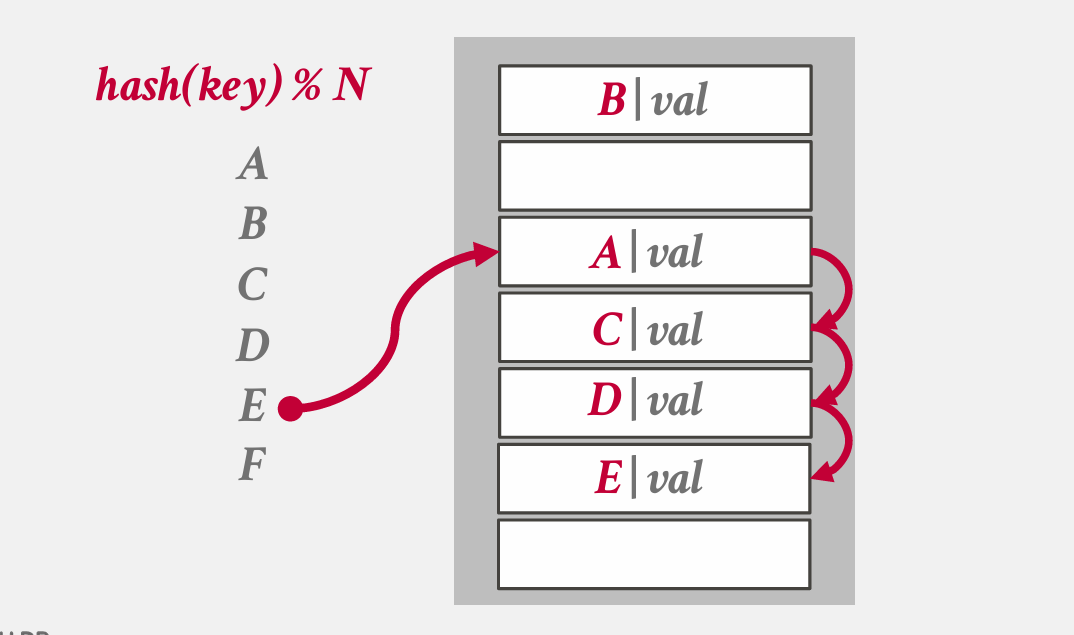
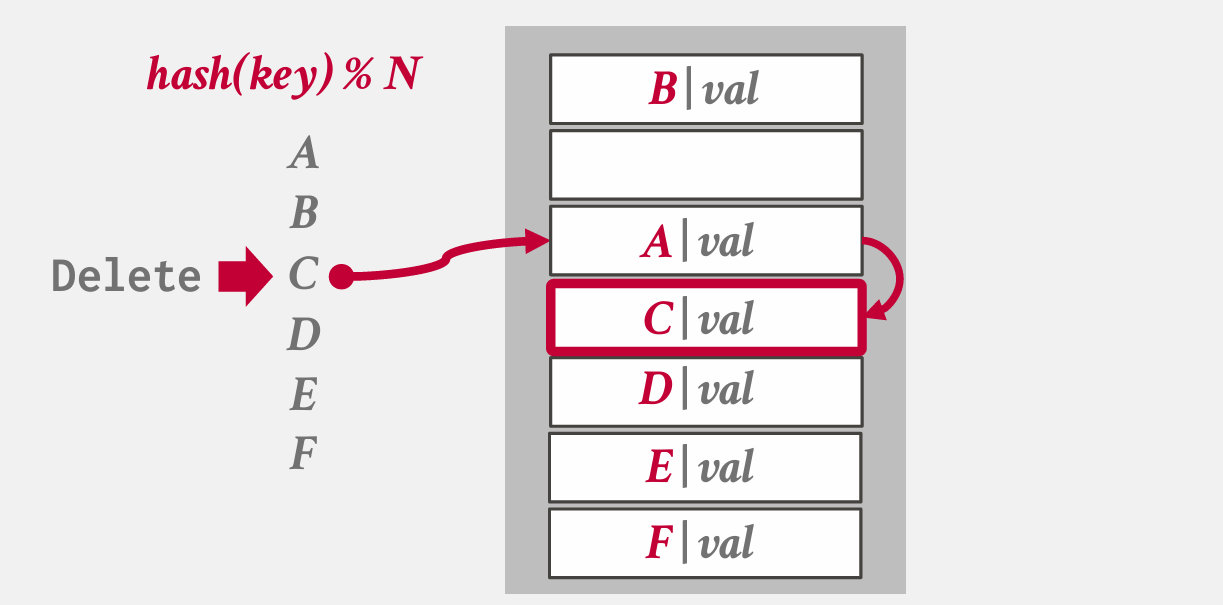
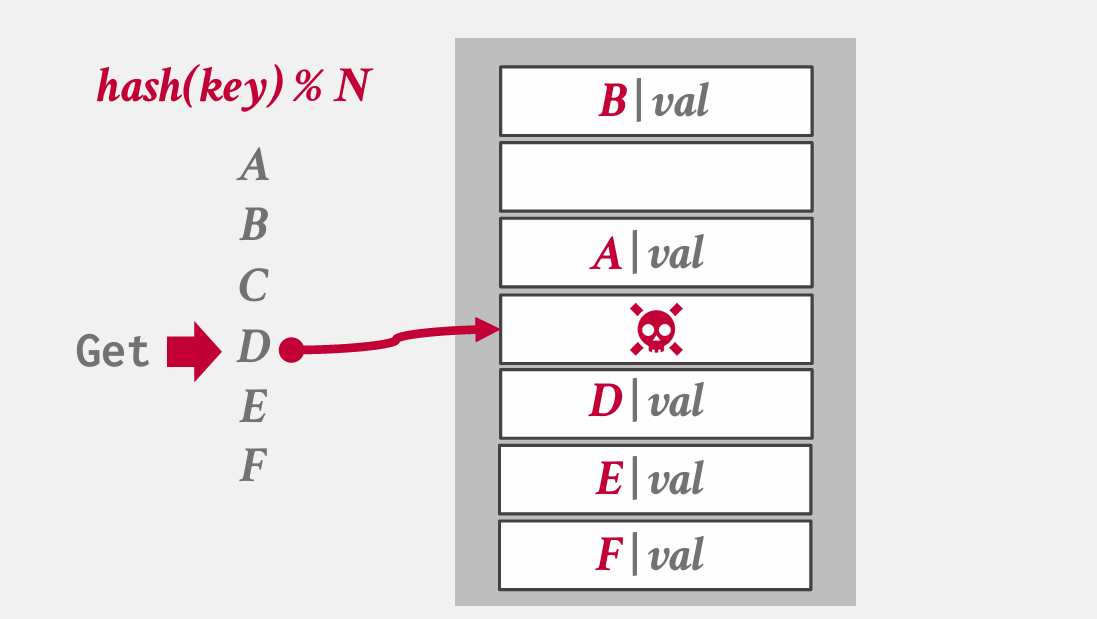
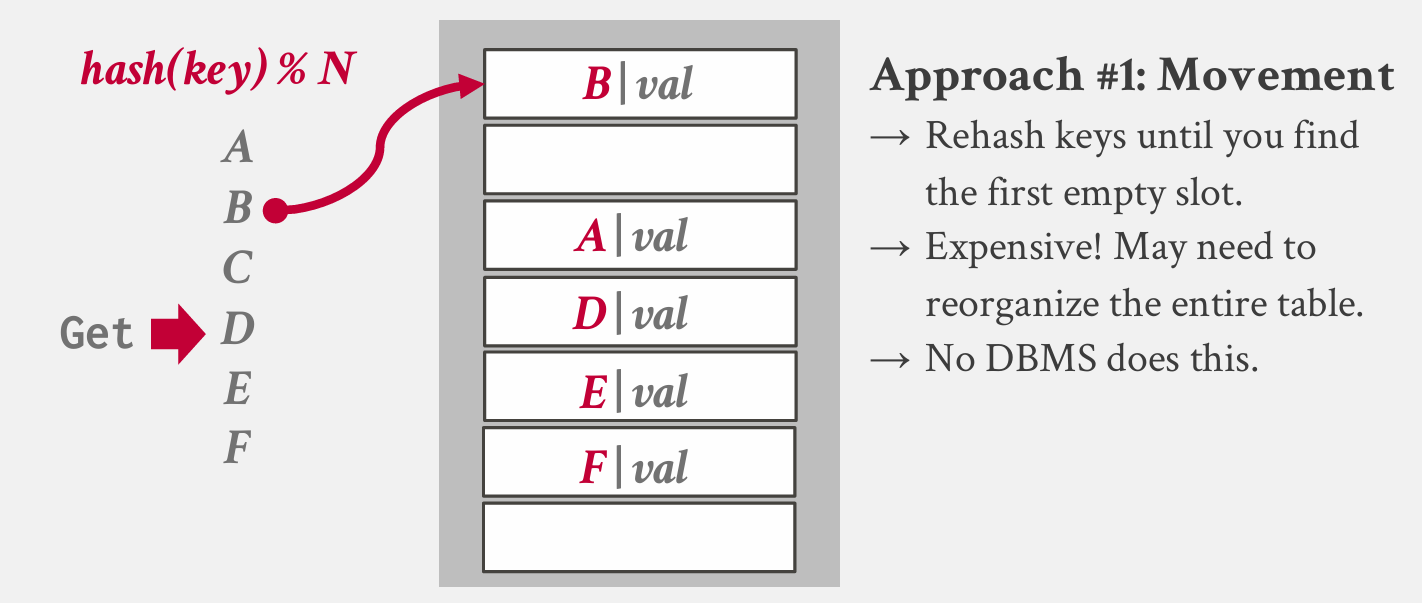
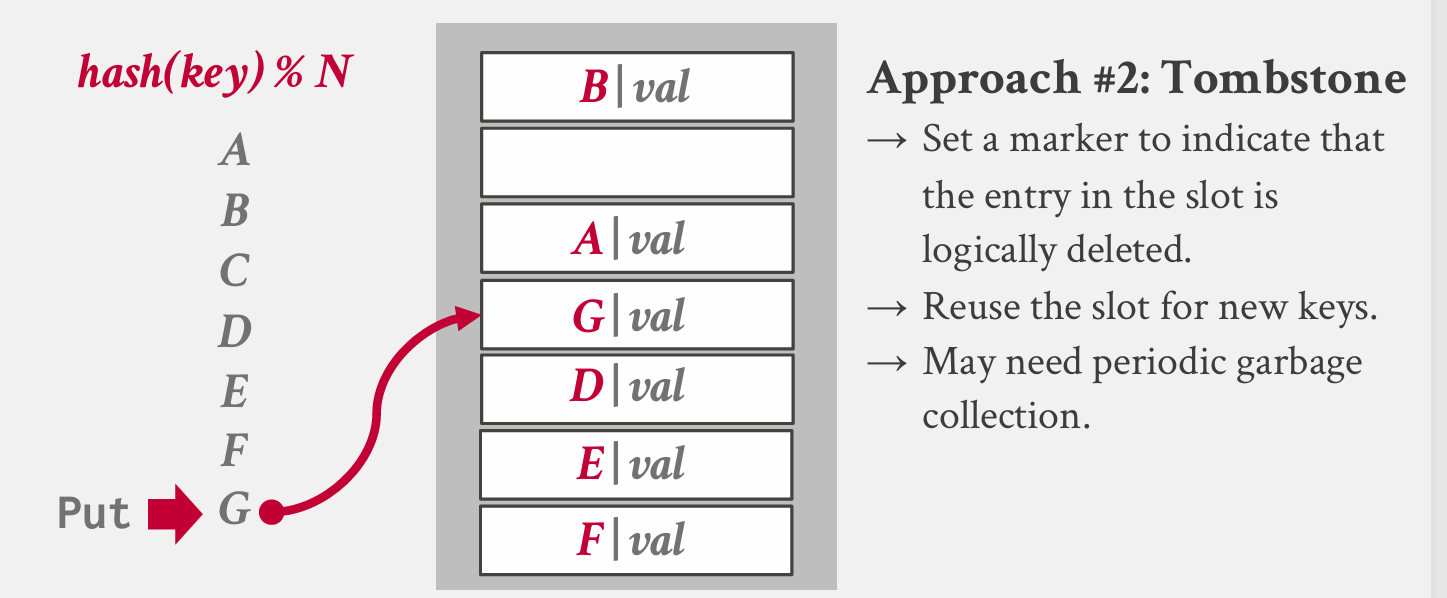
有一个问题，此时查找D，则会找不到——但他实际是在表中的，有多种方法解决这个问题：
- 把所有的数据向上重新hash，直到下一次hash是一个空slot/他自己
- 所以不移动B
- 非常昂贵的操作
- tombstone 墓碑标记
- 浪费空间
- 稍后需清理墓碑
Robin hood hashing
基于线性探测哈希。保存一个所在位置与计算出的位置的距离差，counter越大代表越poor。我们会试着对整个hash table进⾏平衡，劫富济贫，试着让每个key尽可能靠近它原本所在的位置
具体实现方法是，再插入时查看当前元素与下一个元素哪个更poor，距离差更大的会直接使用该位置。例如：
于是：
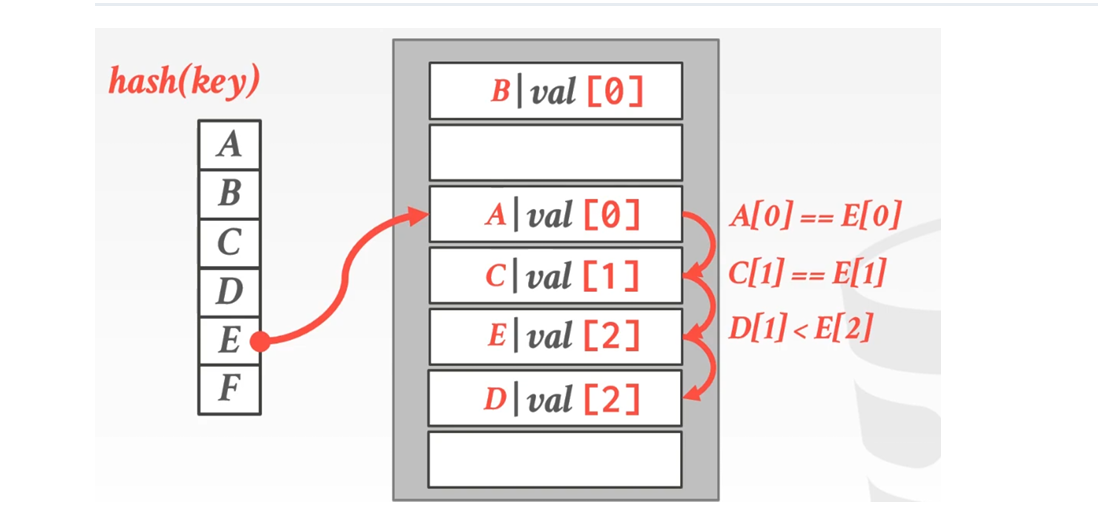
这看起来很nice，但⾄少，现代研究表明，尤其是对内存中的数据结构来说，只要有⼀次条件误判，你就会付出巨⼤的代价。因为在基于 Robin Hood Hashing算法的情况下，我们需要对更多的条件进⾏检查，看看能否将 ⼀个放到另⼀个的位置上，这样，我们就要做更多的写⼊操作，这导致更多的缓存⽆效。So，在实战中，linear probing hashing依然碾压⼀切
Cuckoo hashing
布谷鸟喜欢将它⾃⼰的蛋移到别的⻦巢⾥
使用多个不同的哈希函数（一般用两个），或同一个哈希函数但种子不同。
插入：
- hash，哪个有空插入哪个
- 都有空随便插/根据填充因子插
- 都没空随机/根据填充因子删除一个，插入。被删除的元素需要重新插入
- 为识别循环碰撞，需要记录起始元素。出现时需要重建hash表，元素的位置会被改变
查找和删除的时间复杂度始终是O(1)，但插⼊操作的代价可能会更加昂贵
动态哈希
——我们不想在出现循环碰撞或表满时重建整个表
chained hash table/bucket hash table
相同hash值的key放在同一个chain中，chain关联了多个bucket/page
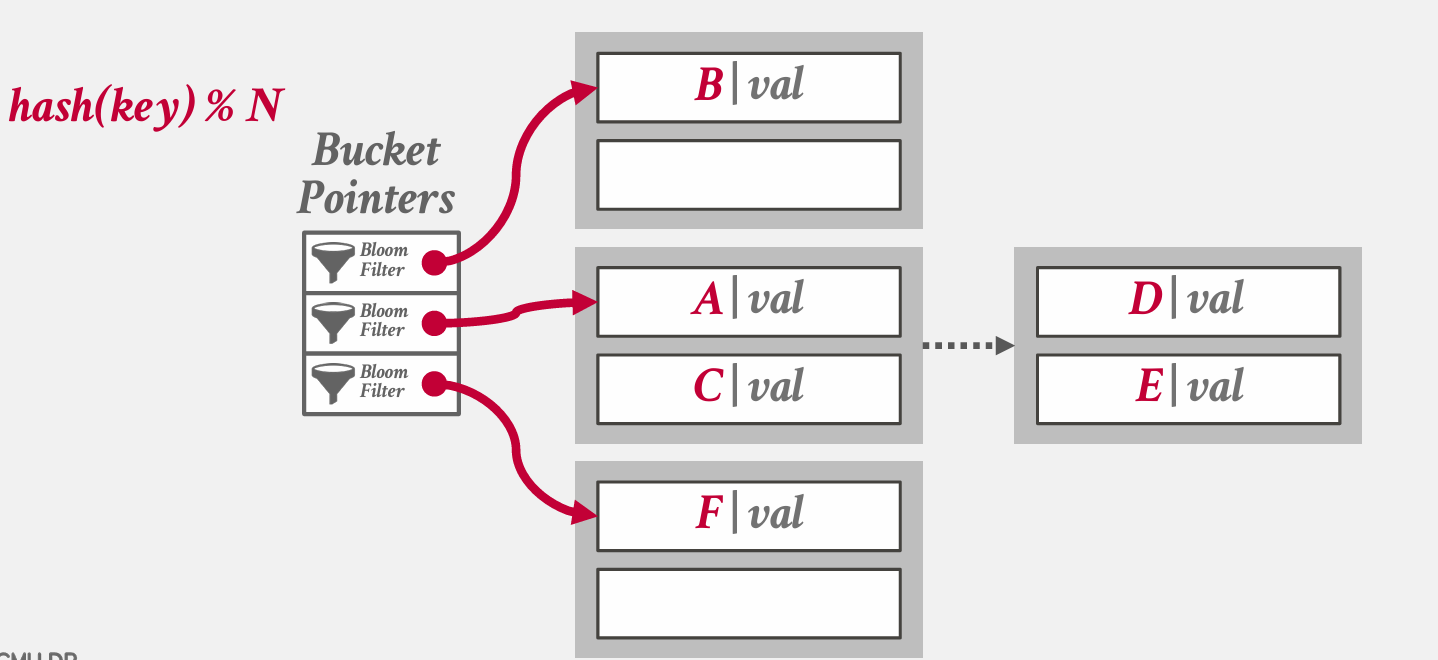
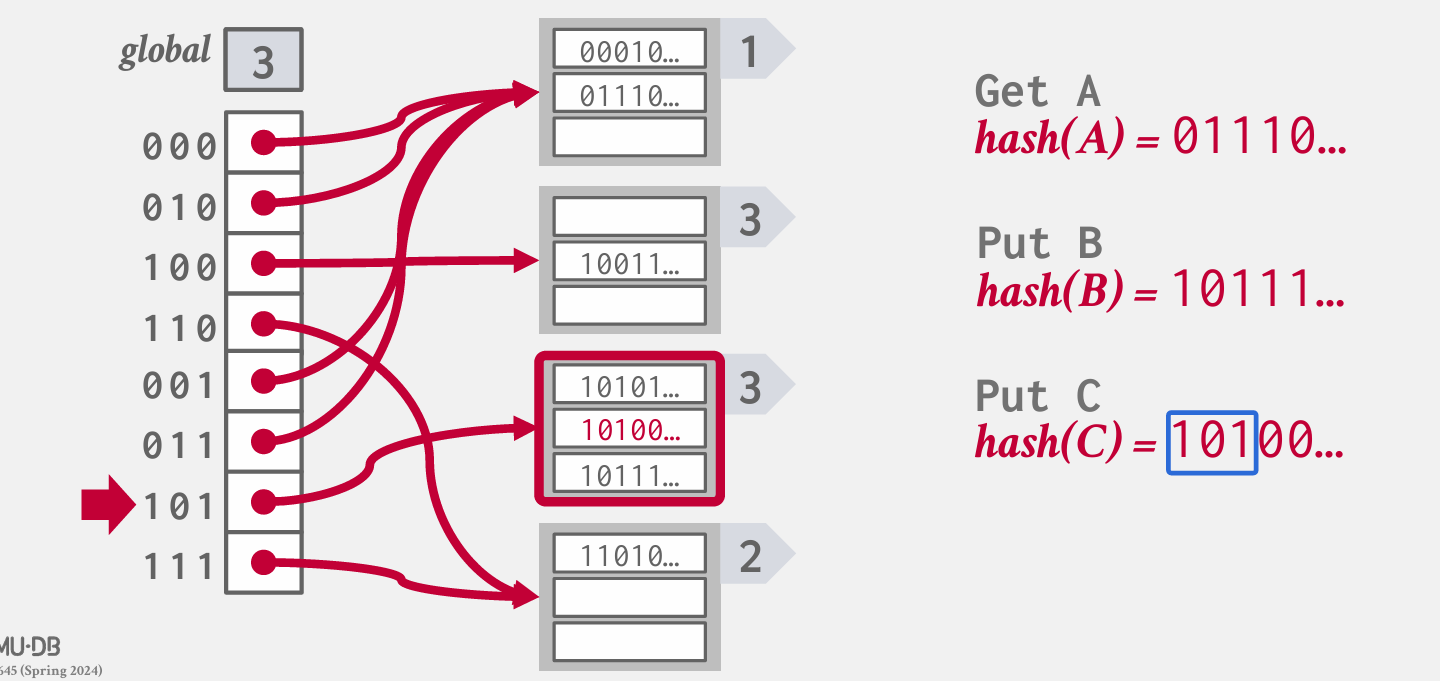
extendible hashing
chain可能过长，我们需要对溢出的bucket进行拆分而不是永远增长下去。
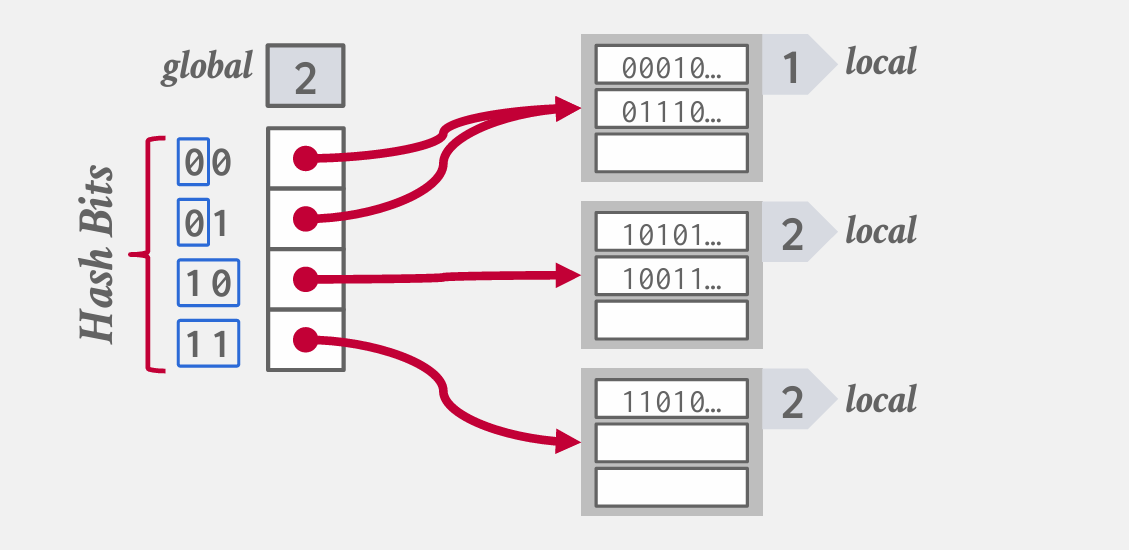
- 全局计数器：查看几位来找到bucket在数组中的的offset
- 局部计数器：本bucket使用的位数，这几位都是相同的
如果像这样溢出：
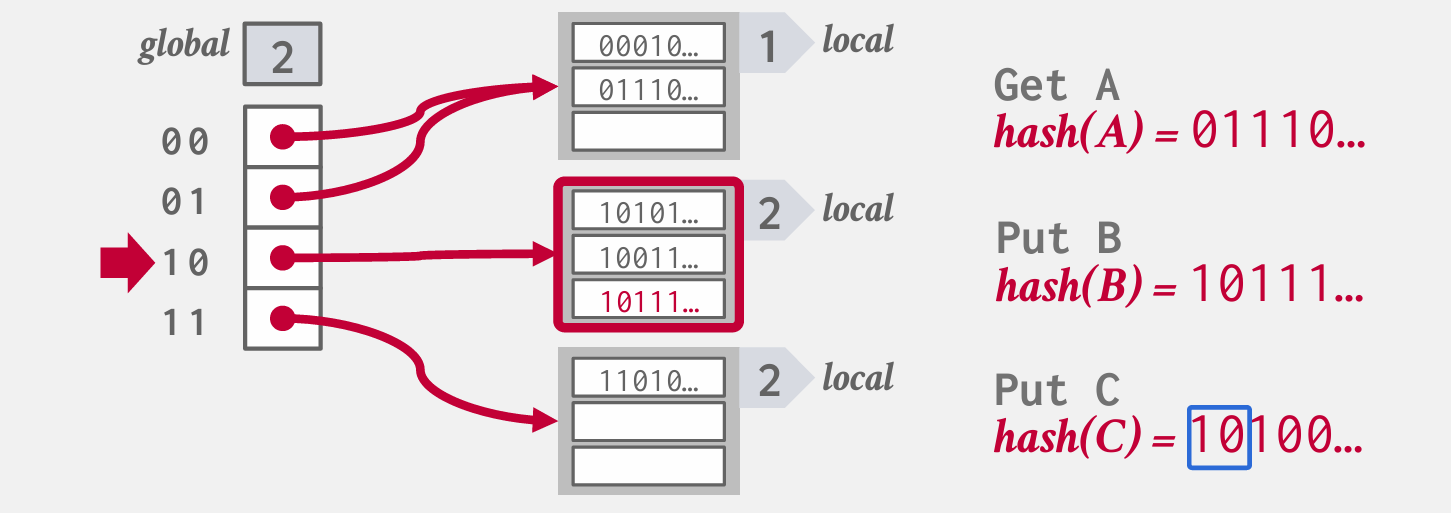
则增加该桶的局部深度，分裂为两个桶、重排元素、重新映射全局目录中的指针
- 若第一个桶溢出，则分裂为00&01两个桶，更新00和01处的指针即可
如果局部桶的深度超过全局，则增加全局深度并映射新添加的目录项
- 本例中，10可分裂为100和101两个桶
- 原指针不变，仍是00、01、10、11的指针，只不过后面加了个0；新项结尾是1。和十进制不同！
linear hashing
..?
渐进式增加全局目录的大小。在某桶溢出时分裂分裂指针指向的桶：2n取模，然后递增分裂指针
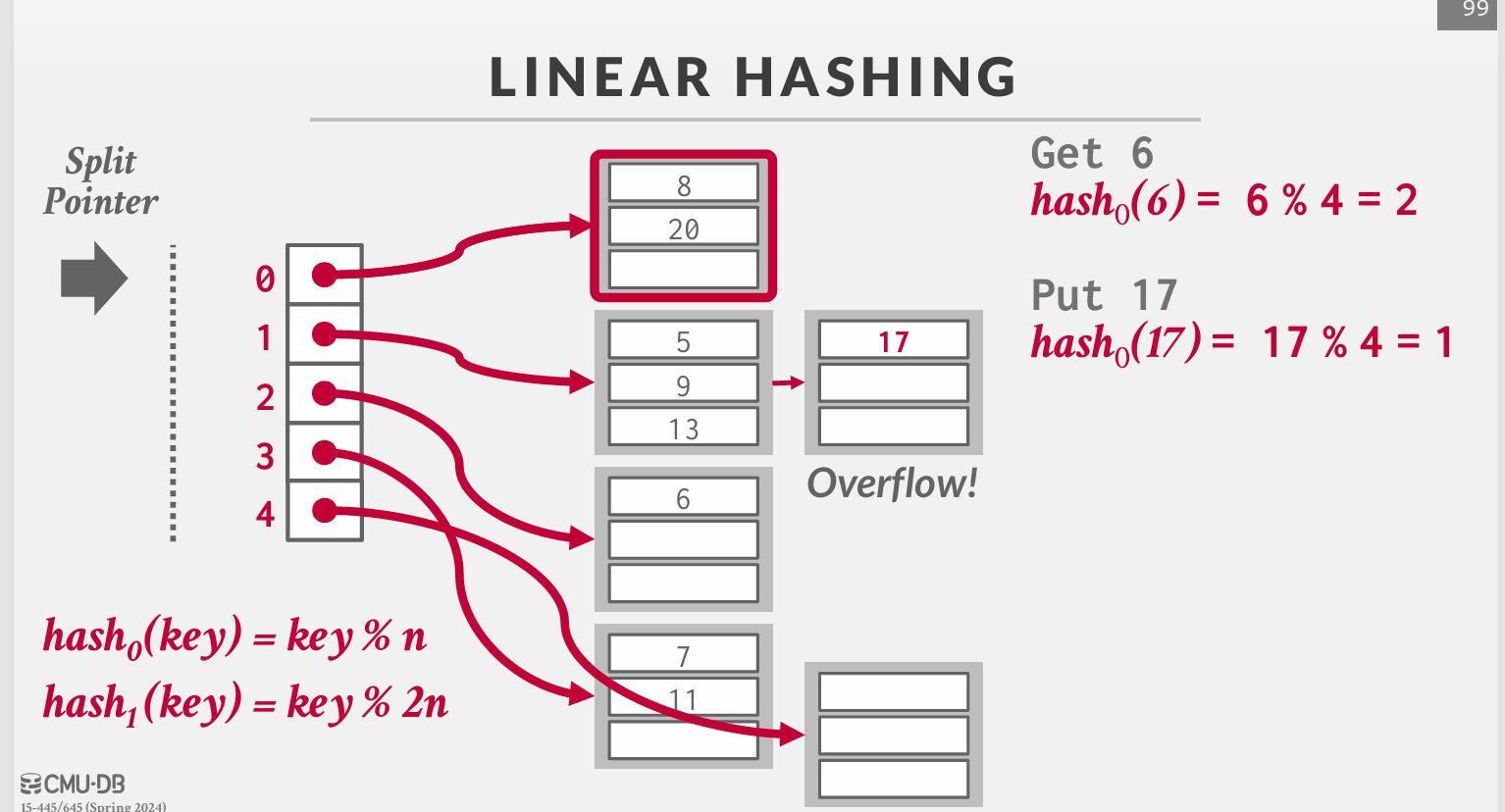
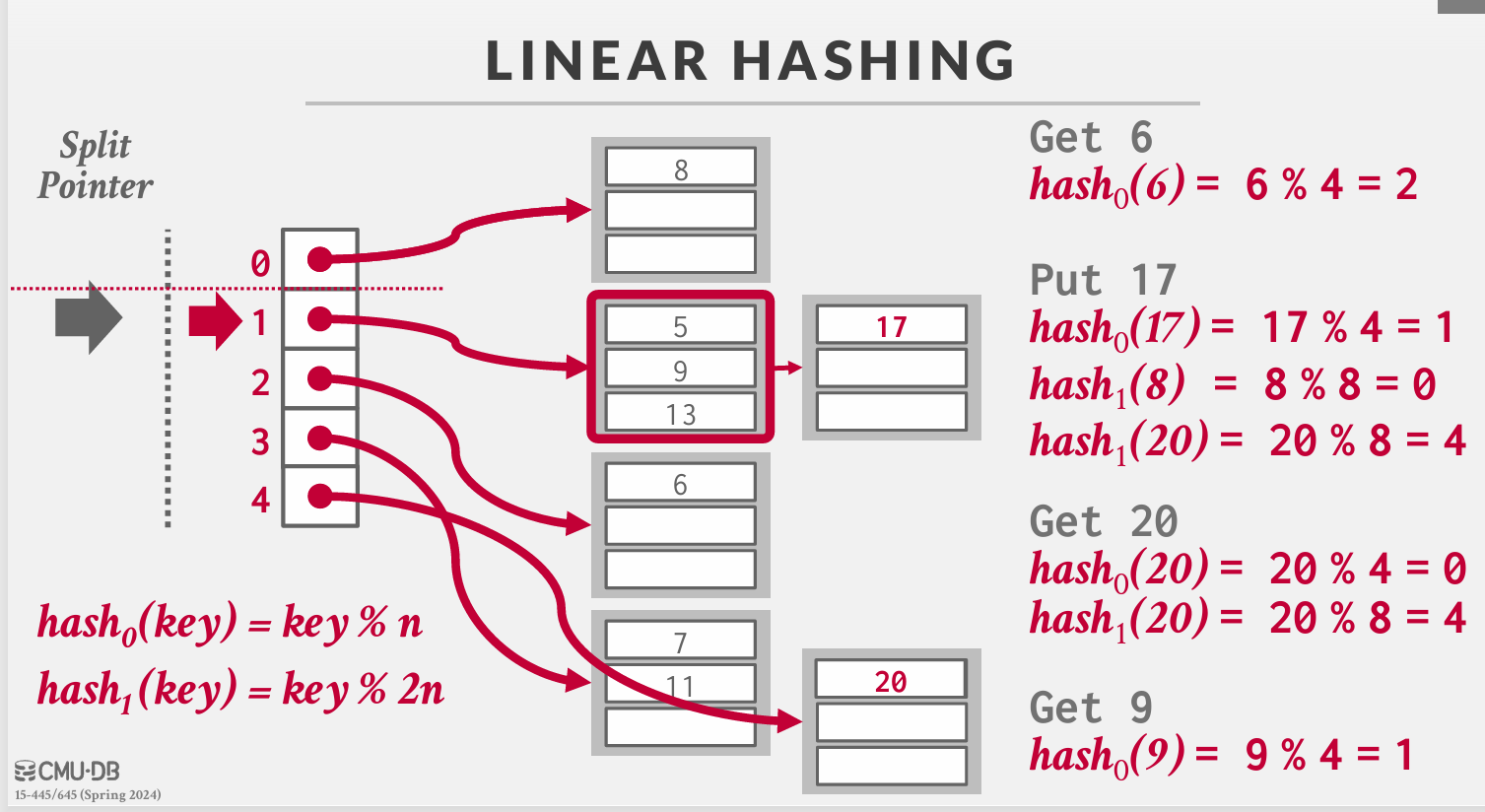
%2n要么分配到原桶，要么分配到新桶
非唯一 key
- 即同一个key有多个对应的值
实现方法： - 链表
- 多次记录重复的key，大部分人的做法
能⽤在我们今天所讲的任何⼀种hashing scheme上
BLOOM FILTERS
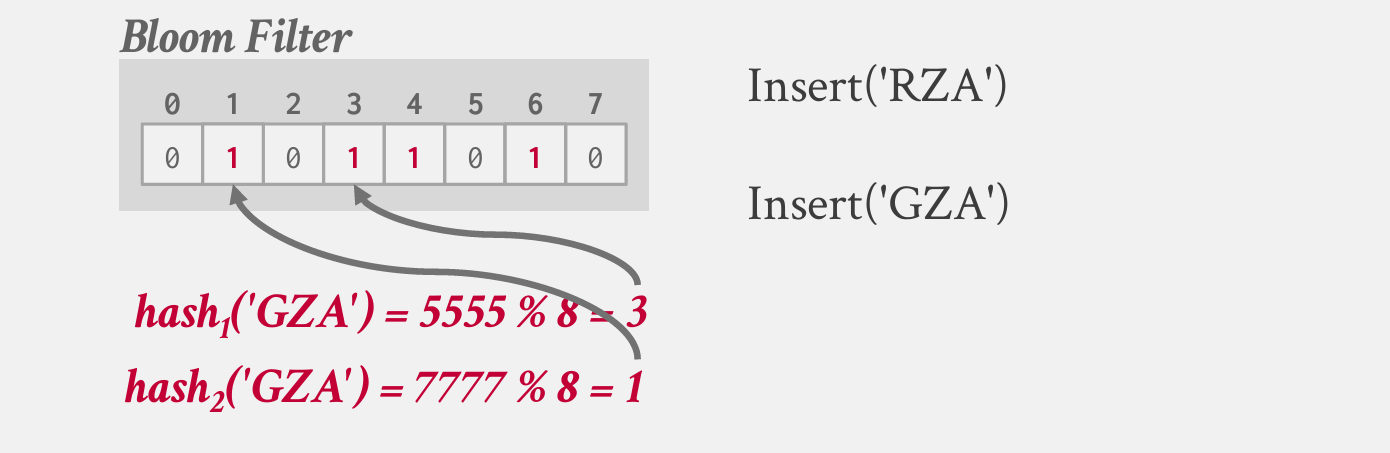
快速测试一个元素是否在一个集合内。存在假阳性但不会有假阴性。使用位数组和多个hash函数表示集合
- 插入：将多个哈希函数计算出的位全设为1
- 查询：计算多个哈希函数的位，若这个位图中的对应位全为1则可能在，不全为1一定不在
