基础算法

暴力/枚举

暴力模拟，码量较大，需要对各个变量、函数的用途有清晰的定义；否则很容易迷失

洛谷P1003 铺毯子

1. 正常的思路是提供一个二维数组，然后对于每个数据更新所指定的矩形区域的编号，但这样的复杂度特别高
2. 但是注意到，只需要求一个点的毯子编号，于是可以先记录下所有的数据，然后遍历一遍求结果
3. 而且因为后来者居上，可以倒着求

力扣59 螺旋矩阵

• 关键点在于使用四个边界变量
• 以及定义清晰各个变量的用途、临界条件

洛谷P1328 石头剪刀布plus

• 打个表定输赢关系
• 另外两个人出拳的周期不同，可以定义一个函数专门处理下一个出什么拳

前缀和 & 差分

核心目的在于避免重复计算，复用从前的运算结果

二维前缀和的计算公式为：​​​$sum_{i,j} = sum_{i-1,j}+sum_{i,j-1}-sum_{i-1,j-1}+a_{i,j}$

• 需要特殊处理0处的元素，为此0行0列全部初始化为0，不放实际数据

利用和数组可以求出特定位置的元素：$a_{i,j}=sum_{i,j}-sum_{i-1,j}-sum_{i,j-1}+sum_{i-1,j-1}$

• 即差分

常见的情形有：

1. n个数，求任意[l,r]的和
   • 遍历一遍求和数组，然后sum[j] - sum[l-1]
   • 同样要留一个位置放0
2. n*n个数，求(x1,y1)到(x2,y2)矩形区域的和(x1<x2,y1<y2)
   • 先求sum数组，然后 $ans=sum[x2][y2]-sum[x2][y1-1]+sun[x1-1][y1-1]-sum[x1-1][y2]$
3. 差分标记：对数组[l,r]范围内所有元素进行m次加某个随机的数q，求最终的数组
   • 利用求和数组的特性，定义一个标记数组，mark[l]+=q，mark[r+1]=-q
   • m次均使用此方法，最后对其求和，加到原数组上
4. 上述题目的二维情形
   • 还是求和数组的特性，求和可以看作影响从自身开始的往右往下所有的求和点
   • $mark[x1][y1] += q$
   • $mark[x1][y2+1] -= q$
   • $mark[x2+1][y1]-=q$
   • $mark[x2+1][y2+1]+=q$
5. 更高维度的情形原理一样，均为容斥

洛谷B3612 区间和

• 没什么可说的，按上面的思路来就行

洛谷P1387 最大长方形

• 前缀和+枚举
• 从高往低枚举更快

洛谷P3397 地毯

• 上述的情形4

尺取法/滑动窗口/双指针

长度为n的数组有n(n+1)/2个连续子区间，利用双指针法可将枚举时间复杂度降至O(n)。通常用于区间属性单调变化的情形

LCR 008 长度大于k的最小子数组

• 注意需要循环将区间左端点右移

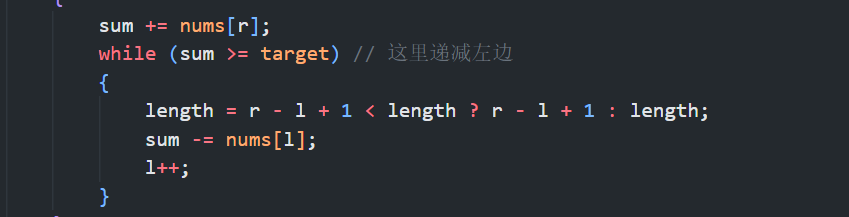
LC 713 成绩小于K的子数组

• 尺取法小于k的情形，每次移动左端点需一次考虑整个区间有多少种满足条件的可能

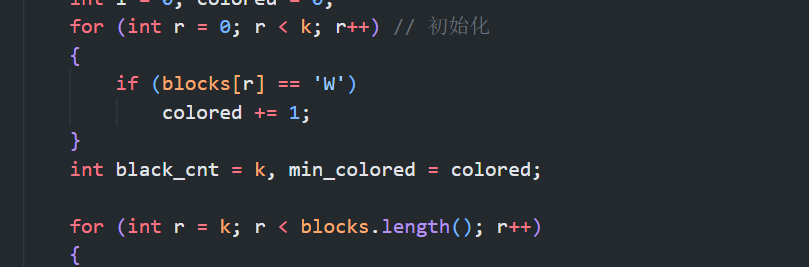
LC 2379 得到K个黑块的最少涂色次数

• 尺取法等于的情形，需要先初始化为k，需要计数定长区间内的涂色次数